[Python] 공분산 구현

python에서는 numpy의 average() 함수를 이용해 공분산을 구현할 수 있다.

 

[In]

# 공분산

%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

x = np.array([50, 70, 40, 60, 80]) # 수학 점수
y = np.array([60, 80, 50, 50, 70]) # 영어 점수
z = np.array([60, 40, 60, 40, 30]) # 국어 점수

cov_xy = np.average((x - np.average(x)) * (y - np.average(y))) # 두 변수의 편차의 곱의 평균
print("-cov_xy :", cov_xy) 

cov_xz = np.average((y - np.average(y)) * (z - np.average(z))) # 두 변수의 편차의 곱의 평균
print("-cov_xz :", cov_xz)

plt.scatter(x, y, marker = 'o', label = 'xy', s = 40) # s는 마커의 크기
plt.scatter(x, z, marker = 'x', label = 'xz', s = 60)
plt.legend()

plt.xlabel('x', size = 14)
plt.ylabel('y', size = 14)
plt.grid()

plt.show()

[Out]

-cov_xy : 120.0
-cov_xz : -72.0

결과를 보게 되면, cov_xy가 양수이므로 x가 커질 때 y도 커지는 것(=양의 상관관계)을 확인할 수 있다.

반면에 cov_xz는 음수이므로, x가 커질 때 z는 작아지는 것(=음의 상관관계)을 확인할 수 있다.

---

 

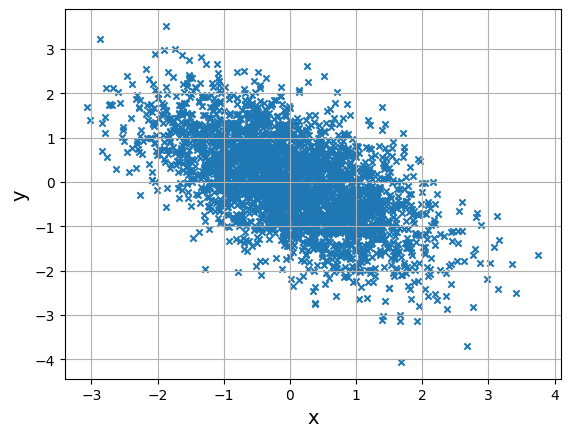
python에서는 numpy의 multivariate_normal() 함수를 이용해 공분산과 정규분포를 통해 데이터를 생성할 수 있다.

첫번째 파라미터에는 확률변수의 평균의 배열, 두번째 파라미터에는 공분산 행렬, 세번째 파라미터에는 데이터의 생성개수가 들어간다.

 

[In]

# 공분산 행렬을 이용한 데이터 생성
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

def show_cov(cov):
    print("--- Covariance :", cov, "---")
    # x, y는 표준정규분포를 따름
    average = np.array([0, 0]) # x와 y의 평균
    cov_matrix = np.array([[1, cov],
                           [cov, 1]]) # 공분산 행렬 지정
    
    # 공분산으로부터 각각 3000개의 x, y의 데이터쌍 생성
    # data는 (3000, 2)의 shape를 가진 행렬
    data = np.random.multivariate_normal(average, cov_matrix, 3000)
    x = data[:, 0] # 첫번째 열을 x로 지정
    y = data[:, 1] # 두번째 열을 y로 지정
    
    plt.scatter(x, y, marker='x', s = 20)

    plt.xlabel('x', size = 14)
    plt.ylabel('y', size = 14)
    plt.grid()
    
    plt.show()
    
show_cov(0.6)  # 공분산 : 0.6
show_cov(0.0)  # 공분산 : 0.0
show_cov(-0.6) # 공분산 : -0.6

[Out]

--- Covariance : 0.6 ---

--- Covariance : 0.0 ---

--- Covariance : -0.6 ---