[Python] 정보량과 엔트로피, 교차 엔트로피 구현

 

python에서 밑이 2인 로그는 numpy의 log2() 함수로 계산이 가능하다.

[In]

# 정보량
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

p = np.linspace(0.01, 1, 1000) # 0일 때 로그는 발산하므로 0.01부터 시작!
y = -np.log2(p)

plt.plot(p, y)

plt.xlabel('p', size = 14)
plt.ylabel('x', size = 14)
plt.grid()

plt.show()

[Out]

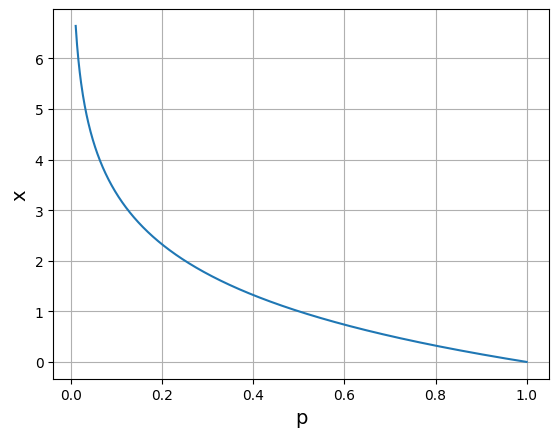
위 그래프와 마찬가지로 정보량은 확률이 작을수록 커지는 것을 확인할 수 있다.

 

[In]

# 베르누이 분포의 엔트로피
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

p = np.linspace(0.01, 0.99) # 0일 때 로그는 발산하므로 0.01 ~ 0.99로 제한

H = -p * np.log2(p) - (1 - p) * np.log2(1 - p) # 베르누이 분포의 엔트로피

plt.plot(p, H)

plt.xlabel('p', size = 14)
plt.ylabel('H', size = 14)
plt.grid()

plt.show()

[Out]

위 그래프와 마찬가지로, p = 0.5일 때 데이터의 불확실성이 매우 크고, 따라서 엔트로피가 가장 큰 것을 확인할 수 있다.

 

[In]

# 베르누이 분포의 교차 엔트로피 계산

import numpy as np

delta = 1e-7 # log() 함수가 0이 되는 것을 방지

# 교차 엔트로피 계산
def cross_entropy(p, t):
    return -np.sum(t*np.log(p + delta) + (1 - t)*np.log(1 - p + delta))

p_1 = np.array([0.2, 0.8, 0.1, 0.3, 0.9, 0.7]) # 정답과 거리가 먼 예측값
p_2 = np.array([0.7, 0.3, 0.9, 0.8, 0.1, 0.2]) # 정답과 거리가 가까운 예측값

t = np.array([1, 0, 1, 1, 0, 0]) # 정답

print("--- 예측과 정답이 떨어져 있는 경우 ---")
print(cross_entropy(p_1, t))
print("--- 에측과 정답이 가까운 경우 ---")
print(cross_entropy(p_2, t))

[Out]

--- 예측과 정답이 떨어져 있는 경우 ---
10.231987952842859
--- 에측과 정답이 가까운 경우 ---
1.3703572638850776

위 결과와 같이, 예측과 정답이 가까울 수록 엔트로피가 작아지는 것을 확인할 수 있다.

뉴럴 네트워크에서는 대상을 분류할 때, 교차 엔트로피가 작아지도록 학습을 시행하면 예측 정밀도가 향상되어 좋은 모델을 생성할 수 있다.