[Python] 단일 뉴런의 학습 구현

이 내용에 들어가기에 앞서, 아래 글을 참고하면 이해하는데 도움이 될 것이다.

https://taichi1.tistory.com/48

[Python] 뉴럴 네트워크(딥러닝) 개요

 

 

 

 

 

데이터 설정

[In]

# 입력 데이터 준비
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt

X = np.linspace(-np.pi/2, np.pi/2, 100) # 입력
T = (np.sin(X) + 1) / 2 # 정답
n_data = len(T) # 정답 개수

# ---- 그래프 그리기 -----
plt.plot(X, T)

plt.xlabel('X', size = 14)
plt.ylabel('T', size = 14)
plt.grid()

plt.show()

[Out]

 

순전파와 역전파 구현

[In]

# 순전파와 역전파
# ---- 순전파 ----
def forward(x, w, b):
    u = x * w + b
    y = 1 / (1 + np.exp(-u))
    
    return y

# ---- 역전파 ----
def backward(x, y, t):
    delta = (y - t) * (1 - y) * y
    grad_w = x * delta # w의 그래디언트
    grad_b = delta # b의 그래디언트
    
    return (grad_w, grad_b)

출력의 표시

[In]

# 출력의 표시
# ---- 출력 그래프 ----
def show_output(X, Y, T, epoch):
    
    plt.plot(X, T, linestyle = 'dashed')
    plt.scatter(X, Y, marker='+', c = 'orange')
    
    plt.xlabel('x', size = 14)
    plt.ylabel('y', size = 14)
    plt.grid()
    
    plt.show()
    
    Error = 1/2*np.sum((Y - T)**2) # 전체 데이터에 대한 제곱 오차
    
    print("Epoch :", epoch)
    print("Error :", Error)

 

 

학습

[In]

# 학습
# ---- 하이퍼 파라미터 설정 ----
n = 0.1 # 학습계수
epoch = 200 # 에포크 수

# ---- 초깃값 ----
w = 0.2 # 가중치
b = -0.2 # 바이어스

# ---- 학습 ----
for i in range(epoch):
    if i < 10: # 최초 9 epoch 까지 표시
        Y = forward(X, w, b)
        show_output(X, Y, T, i)
        
    idx_rand = np.arange(n_data) # 0 ~ n_data - 1 까지의 정수를 array로 변환
    np.random.shuffle(idx_rand) # array를 랜덤으로 섞음
    
    for j in idx_rand:
        x = X[j] # 입력 데이터
        t = T[j] # 라벨 데이터
        
        y = forward(x, w, b) # 순전파
        grad_w, grad_b = backward(x, y, t) # 역전파
        w -= n * grad_w # 가중치 갱신
        b -= n * grad_b # 바이어스 갱신

# ---- 학습 후 결과 표시 ----
Y = forward(X, w, b)
show_output(X, Y, T, epoch)

[Out]

Epoch : 0
Error : 4.944806846912912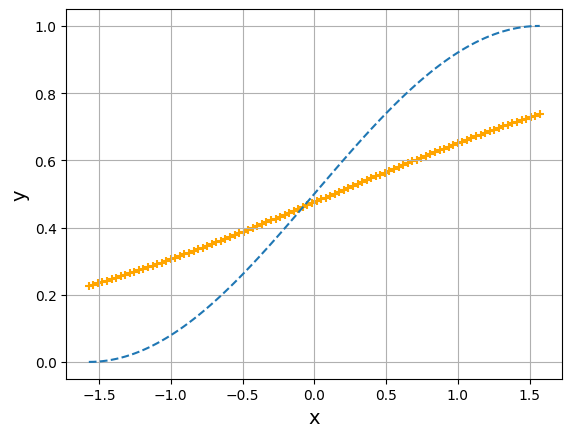

Epoch : 1
Error : 2.0541666844664883

Epoch : 2
Error : 1.1007980214734048

Epoch : 3
Error : 0.6889275876089423

Epoch : 4
Error : 0.47235597367961873

Epoch : 5
Error : 0.34377702111945346

Epoch : 6
Error : 0.2610639372345687

Epoch : 7
Error : 0.20465321994912405

Epoch : 8
Error : 0.16451422531689824

Epoch : 9
Error : 0.13499632036343762

 

Epoch : 200
Error : 0.018720802097614214

 

결과를 보게 되면, 학습이 진행됨에 따라 Error가 점점 감소하는 것을 알 수가 있다.